Generating the multiplication table for octonions in Odin
Date written: 2022.08.29
I only recently learned a method to think about the multiplication of octonions that is both simple and satisfying. When octonions are thought of as pairs of quaternions, octonion multiplication reduces to a simple formula which can be trivially implemented in any decent programming language. We do this below in the Odin programming language, and generate the same multiplication table for octonions on Wikipedia.
For most of my childhood the octonions seemed mysterious. I don't know the exact date I first heard about them, but it was as far back as middle school. I knew they were related to each other as important extensions to the real numbers, but I didn't know their basic properties — such as how they multiply. I certainly didn't know about their relationship to other areas of mathematics.
Octonion multiplication is actually related to complex number multiplication: the way that octonions can be interpreted as pairs of quaternions extends to interpreting the quaternions as pairs of complex numbers. The process even extends to interpreting complex numbers as pairs of real numbers. In other words, starting with the real numbers, the complex numbers, the quaternions, and the octonions can be successively built from each other. This construction is known as the Cayley-Dickson construction. If you know how to add and multiply real numbers, the construction says you can understand how to add and multiply octonions too.
We illustrate the Cayley-Dickson construction with examples below. We first show how to obtain the quaternions from the complex numbers. We then show how to obtain the octonions from the quaternions. We generate an octonion multiplication table by writing a simple program in Odin, a new(ish) programming language which is an alternative to C. Figuring out this multiplication table by hand would by contrast require 64 calculations. While some computations could be done with shortcuts, generating the table with a computer is a lot less labour-intensive and significantly less error-prone.
Constructing the quaternions from the complex numbers
Let's begin with by using complex numbers to construct the quaternions. The complex numbers are commonly thought of as sums of the form \( a + bi \) where \( a \) and \( b \) are real numbers and the \( i \) satisfies the rules \( 1 \cdot i = i \cdot 1 = i \) and \( i \cdot i = - 1 \), where the · symbol denotes multiplication. Expository mathematics often says that \( i = \sqrt{-1} \) but this is technically inaccurate: there are two solutions to the equation \( x^2 = -1 \) over the complex numbers, so saying \( i = \sqrt{-1} \) without specifying which of the two solutions the \( i \) is equal to is inherently ambiguous. We'll stick with the algebraic description.
Complex numbers come with an operation known as conjugation. The operation sends a complex number of the form \( a + bi \) to the complex number \( a - bi \). If \( z \) is a complex number, its conjugate is usually denoted \( \bar z \). An important property of conjugation is \( \overline{\overline{z}} = z \). We'll use conjugation to construct the quaternions.
The Cayley-Dickson construction is defined abstractly using the language of vector spaces and algebras, but there is no need to use that level of generality here. When applied to the complex numbers, it says the following: the quaternions are pairs of complex numbers where addition of pairs is defined by $$ \begin{equation} (a,b) + (c,d) = (a + c, b + d), \end{equation} $$ multiplication of pairs is defined by $$ \begin{equation} (a,b) \cdot (c,d) = (ac - \bar d b, da + b \bar c), \end{equation} $$ and scalar multiplication of a pair by a real number is defined by $$ \begin{equation} c(a,b) = (ca,cb). \end{equation} $$
There are a few things to note. First, every quaternion is defined by four real variables, since each pair has the form \( (x + yi, z + wi) \) for some real numbers \( x,y,z,w \). Second, the addition and scalar multiplication rules (1) and (2) together imply that $$(x + yi, z + wi) = x(1,0) + y(i,0) + z(0,1) + w(0,i).$$ So in the same way that every complex number is a sum of multiples of \( 1 \) and \( i \), every quaternion is a sum of multiples of \( (1,0),(i,0),(0,1),(0,i) \).
Let's address the seemingly bizarre multiplication rule that is equation (2). Why on earth would we even expect it to work? For starters, the multiplication rule is bilinear, although this is not obvious from the equation. Bilinearity means it satisfies two natural properties.
First, if \( f,g,h \) are quaternions, then \( f \cdot (g + h) = f \cdot g + f \cdot h \). This property is satisfied if \( f,g,h\) are simply real or complex numbers. A simple calculation using equations (1) and (2) shows that the quaternions satisfy the property too, meaning that quaternion multiplication distributes over quaternion addition.
Secondly, if \( r \) is a real number and \( x, y \) are quaternions, then \( (rx) \cdot y = r(x \cdot y ) \). This property holds when \( x, y \) are real or complex numbers, and proving that it holds for quaternions involves a few short algebraic calculations using equations (1) and (2) as well.
An upside of bilinearity is that it makes multiplication easier. Every quaternion is a sum of multiples of \( { (1, 0), (i, 0), (0, 1), (0, i) } \), so bilinearity means that quaternion multiplication in general is determined by how these pairs multiply together.
As an example, equation (2) says $$(i,0) \cdot (0,1) = (i \cdot 0 - \bar 1 \cdot 0, 1 \cdot i + 0 \cdot \bar 0) = (0,i).$$ We can similarly do 15 other calculations and obtain the following table.
| \( x \cdot y \) | \( y \) | ||||
| \( (1, 0) \) | \( (i, 0) \) | \( (0, 1) \) | \( (0, i) \) | ||
| \( x \) | \( (1, 0) \) | \( (1, 0) \) | \( (i, 0) \) | \( (0, 1) \) | \( (0, i) \) |
| \( (i, 0) \) | \( (i, 0) \) | \(-(1, 0) \) | \( (0, i) \) | \(-(0,1) \) | |
| \( (0, 1) \) | \( (0, 1) \) | \( -(0, i) \) | \( -(1, 0) \) | \( (i, 0) \) | |
| \( (0, i) \) | \( (0, i) \) | \( (0, 1) \) | \( -(i, 0) \) | \( -(1,0) \) | |
People who are familiar with the quaternions might find the table above far removed from the common definition of the quaternions, but the two are actually very close! Setting $$ \begin{equation} \begin{split} (1,0) &= 1 \\ (i, 0) &= i \\ (0, 1) &= j \\ (0, i) &= k \end{split} \end{equation} $$ transforms the table as follows.
| \( x \cdot y \) | \( y \) | ||||
| \( 1 \) | \( i \) | \( j \) | \( k \) | ||
| \( x \) | \( 1 \) | \( 1 \) | \( i \) | \( j \) | \( k \) |
| \( i \) | \( i \) | \(-1 \) | \( k \) | \( -j \) | |
| \( j \) | \( j \) | \( -k \) | \( -1 \) | \( i \) | |
| \( k \) | \( k \) | \( j \) | \( -i \) | \( -1 \) | |
This is the standard multiplication table for the quaternions. In particular, it produces the well-known equations $$ \begin{equation} i^2 = j^2 = k^2 = ijk = -1 \end{equation} $$ which Hamilton carved into the Broom Bridge in Dublin when he came up with the formula.
The Cayley-Dickson construction also gives us a notion of conjugation on pairs. This is defined as $$ \begin{equation} \overline{(a,b)} = (\bar a, -b ). \end{equation} $$ For example, $$ \bar k = \overline{(0,i)} = (\bar 0, -i) = -(0, i) = -k. $$ Similar calculations can be done to give $$ \begin{equation} \begin{split} \bar 1 &= 1, \\ \bar i &= -i, \\ \bar j &= -j, \\ \bar k &= -k. \end{split} \end{equation} $$
So we have constructed the quaternions from the complex numbers by interpreting them as pairs, and know how they add, multiply, and conjugate.
Constructing the octonions from the quaternions
We can now apply the Cayley-Dickson construction to the quaternions using the exact same equations we used to construct the quaternions — equations (1), (2), (3), (5). This time, we'll implement the construction in Odin. The final file with our Odin code is available here.
Implementing an integer quaternion type
Let us first define an integer quaternion type. Odin already has support for quaternions as floats, but we will not use them since floats are inherently imprecise. The exposition will also be clearer if we just work with integers.
At the top of a blank file, we'll import an Odin module to format the multiplication table, and then define our quaternion and octonion data types.
package octonions
import "core:fmt"
quat :: [4] int // Our 'integer' quaternion type.
oct :: [2] quat // Our 'integer' octonion type.
The :: syntax used above is used to define data types, procedures, structs and constants in Odin. The [N] type syntax denotes a fixed-length array of type type. We can now define a basis of quaternions we'll use to perform calculations.
// Standard basis for the quaternions.
id :: quat{ 1, 0, 0, 0}
i :: quat{ 0, 1, 0, 0}
j :: quat{ 0, 0, 1, 0}
k :: quat{ 0, 0, 0, 1}
zq :: quat{ 0, 0, 0, 0}
The bilinearity of the product in the Cayley-Dickson construction tells us that a basis for the octonions will be given by all possible pairs of the zero vector and one of the quaternion basis vectors. In other words, the following constitute a basis for the octonions.
// Create the standard basis for the octonions (from Cayley-Dickson construction).
a :: oct{id, zq }
b :: oct{ i, zq }
c :: oct{ j, zq }
d :: oct{ k, zq }
e :: oct{ zq, id}
f :: oct{ zq, i }
g :: oct{ zq, j }
h :: oct{ zq, k }
The Cayley-Dickson octonion product requires us to multiply, add and conjugate quaternions. So we must first define these procedures for our integer quaternions types.
For addition, we don't actually have to write a custom procedure. By default, fixed-length arrays in Odin already come with addition, subtraction and scalar multiplication operations. These are overloaded onto the +, -, * operations for numerical data types.
For example, the following code does not cause a run-time error.
// Automatic overloading of +,-,* for fixed-length numerical arrays.
assert(id + 2*i + 3*j + 4*k == quat{1,2,3,4})
We can figure out a procedure for quaternion multiplication with some simple algebra. The product of the quaternions \( a + bi + cj + dk \) and \( e + fi + gj + hk \) (where \( a,b,c,d,e,f,g,h \) are real numbers) is simple enough to compute by hand. The result is incorporated into the following procedure.
// Simple quaternion multiplication.
qm :: proc( x,y : quat ) -> (z : quat ) {
a, b, c, d : = x[0], x[1], x[2], x[3]
e, f, g, h : = y[0], y[1], y[2], y[3]
z[0] = a*e - b*f - c*g - d*h
z[1] = a*f + b*e + c*h - d*g
z[2] = a*g + c*e + d*f - b*h
z[3] = a*h + d*e + b*g - c*f
return
}
Note our use of Odin's ability to handle declarations with multiple values. Specifically, there is no need to put a = x[0] and b = x[1] on different lines. In the first and second lines of the procedure body, the compiler is smart enough to assign the four variables on the left of the = sign with the corresponding integers on the right hand side. Additionally note that the procedure simply ends with return instead of the more traditional return and its value — we instead gave the return value a name (z) and assigned its values in the body of the procedure.
We previously showed that quaternion conjugation is very simple.
// Simple quaternion transpose.
qt :: proc ( x : quat ) -> ( z : quat ) {
z[0], z[1], z[2], z[3] = x[0], -x[1], -x[2], -x[3]
return
}
Before we use the above procedures to write an octonion multiplication procedure, we should check that they work!
// Testing of quaternion multiplication procedures.
fmt.println("Testing multiplication of standard basis i,j,k...")
fmt.println("ij == k:", qm(i,j) == k)
fmt.println("jk == i:", qm(j,k) == i)
fmt.println("ki == j:", qm(k,i) == j)
fmt.println("ijk == -1:", qm(qm(i,j),k) == -1*id)
fmt.println("j * {1,2,3,4} == {-3,4,1,-2}:",
qm(j,quat{1,2,3,4}) == quat{-3,4,1,-2})
Evoking the terminal command odin run filename -file compiles and then runs filename. In our case, we get
$ odin run .\octonions.odin -file
Testing multiplication of standard basis i,j,k...
ij == k: true
jk == i: true
ki == j: true
ijk == -1: true
j * {1,2,3,4} == {-3,4,1,-2}: true
$
so all our checks passed.
Implementing octonion multiplication and generating a multiplication table
It's time to define octonion multiplication. We just have to implement the Cayley-Dickson multiplication formula (2) using the procedures we defined above.
// octonion multiplication, defined using the standard multiplication from Cayley-Dickson
om :: proc ( x, y : oct) -> ( z : oct) {
a, b := x[0], x[1]
c, d := y[0], y[1]
z[0] = qm(a,c) - qm(qt(d),b)
z[1] = qm(d,a) + qm(b,qt(c))
return
}
Now it's time to create a multiplication table. We'll keep things simple by not worrying about table formatting just yet. We'll add in formatting code at the end.
Let us first define the symbols in the table that will represent the basis elements of the octonions. It's traditional to use \( e_i \), but when we look at sums of these, we only really care about the subindex. Making the subindex smaller and adding in the filler of the symbol \( e \) is unnecessary, so we'll just refer to our basis elements with the characters \( 0, 1, \ldots 7 \). To reiterate, these represent the indices of the basis elements, NOT the integers.
Defining a map in Odin for this symbolic conversion is trivial.
// Create a map from the octonions to the letters they represent. basis_char_map := make(map[oct] rune) basis_char_map[a] = '0' basis_char_map[b] = '1' basis_char_map[c] = '2' basis_char_map[d] = '3' basis_char_map[e] = '4' basis_char_map[f] = '5' basis_char_map[g] = '6' basis_char_map[h] = '7'
Time to generate the table entries! The product in the i-th row and the j-th column of the table will be \( e_i \cdot e_j \). We can iterate through these products with a simple double loop.
fmt.println("A simple octonion multiplication table:")
for ei in basis_char_map {
fmt.println("")
for ej in basis_char_map {
prod := om(ei, ej)
// Code to express product in the basis.
// ...
}
}
The products have been computed, but we need to figure out how to write them a sum of the octonion basis \( e_i \). Here we can apply a trick to greatly simplify matters, which is to guess that for our basis, we will have \( e_i \cdot e_j = \pm e_k \). This is not true for most choices of basis! But it was true for the intuitive basis we picked when we constructed the quaternions, so we can at least see if the property holds in the octonions too. If a product is not of this form, we'll print out an error.
// Code to express product in the basis.
// Assume the product will be of the form +- e_k.
char_p, pos_ok := basis_char_map[prod]
char_n, neg_ok := basis_char_map[-1*prod]
if pos_ok { fmt.printf(" %c ", char_p) }
if neg_ok { fmt.printf("-%c ", char_n) }
if !pos_ok && !neg_ok {
fmt.println("\nERROR: A product was not of the form +- e_k !")
}
If basis_char_map contains prod then pos_ok will be set to true, otherwise it will be set to false. Likewise for neg_ok. If both pos_ok and neg_ok are false, we'll print an error message. Luckily, when we compile and run our program, we get no error messages and a full multiplication table!
$ odin run .\octonions.odin -file A simple octonion multiplication table: 0 1 2 3 4 5 6 7 1 -0 3 -2 5 -4 -7 6 2 -3 -0 1 6 7 -4 -5 3 2 -1 -0 7 -6 5 -4 4 -5 -6 -7 -0 1 2 3 5 4 -7 6 -1 -0 -3 2 6 7 4 -5 -2 3 -0 -1 7 -6 5 4 -3 -2 1 -0 $
When this table is compared to Wikipedia's octonion multiplication table (below, screenshot taken from here), it's easy to see that the numbers match up. In other words, we have generated the canonical multiplication table for the octonions!
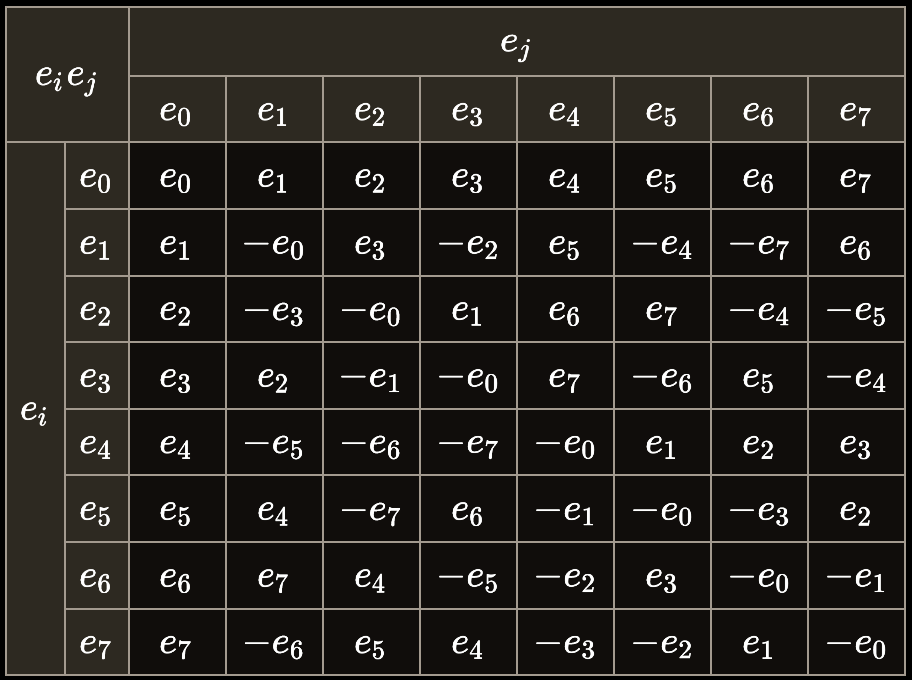
With a bit more work a couple of hours of formatting programming, we can make the program output a formatted ascii table with labels.
$ odin run .\octonions.odin -file A formatted octonion multiplication table: --------------------------------------------------- | | y | - x*y ----------------------------------------- | | 1 | i | j | k | a | b | c | d | --------------------------------------------------- | | 1 | 1 i j k a b c d | | | i | i -1 k -j b -a -d c | | | j | j -k -1 i c d -a -b | | x | k | k j -i -1 d -c b -a | | | a | a -b -c -d -1 i j k | | | b | b a -d c -i -1 -k j | | | c | c d a -b -j k -1 -i | | | d | d -c b a -k -j i -1 | --------------------------------------------------- $
Here we changed the character map to write the basis elements using the symbols \( 1, i, j, k, a, b, c, d \). Note how the entries in each of the four quadrants have similar groupings of symbols. In particular, note how the first four rows and columns form a subtable which is just quaternion multiplication. (And that the first two rows and columns of that form a subtable which is complex multiplication.)
And so we've done what we set out do do! We generated the multiplication table for the octonions without doing any tedious computations by hand, and without errors. The table seemingly has a lot of data, but it can be reduced to a simple diagram by way of the Fano plane.
Just as the quaternion multiplication table can be summarized in a simple line of equations as in (5) above, the content of the octonion multiplication table can be summarized in the following diagram.
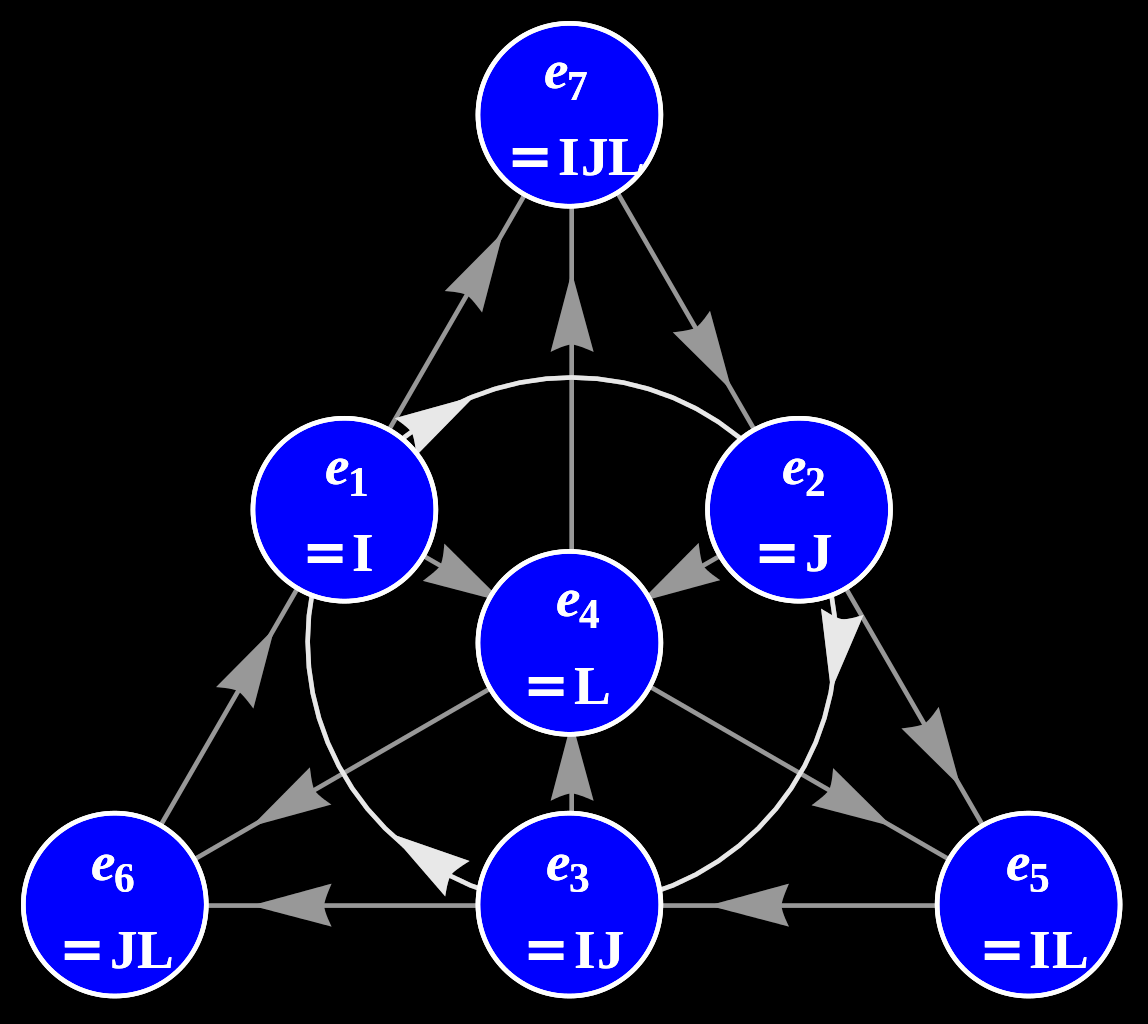
Image credit: Jgmoxness (CC BY-SA 3.0)
To calculate the product \( e_i \cdot e_j \) using this diagram, find the two nodes containing \( e_i \) and \( e_j \), and then locate the unique line or circle which goes through them. The other node on the line or circle will be the product, up to a sign change. To determine the sign, treat each line / circle like the quaternions, and use the corresponding sign convention. If \( e_i = e_j \), the product is \( -1 \). It's much easier to memorize this diagram than the table!
As noted earlier, a link to the .odin file with all the code above can be found here. Running the command odin run .\octonions.odin -file will compile and run the code, which produces the tables and tests shown above.